이진 탐색(C언어)

이진 탐색이란?

이진 검색 알고리즘(binary search algorithm)은 오름차순으로 정렬된 리스트에서 특정한 값의 위치를 찾는 알고리즘이다. 처음 중간의 값을 임의의 값으로 선택하여, 그 값과 찾고자 하는 값의 크고 작음을 비교하는 방식을 채택하고 있다.

처음 선택한 중앙값이 만약 찾는 값보다 크면 그 값은 새로운 최댓값이 되며, 작으면 그 값은 새로운 최솟값이 된다.

검색 원리상 정렬된 리스트에만 사용할 수 있다는 단점이 있지만, 검색이 반복될 때마다 목표값을 찾을 확률은

두 배가 되므로 속도가 빠르다는 장점이 있다.

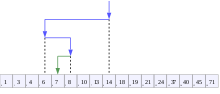
정렬이 되어 있는 배열이 필요하기 때문에 병합 정렬로 먼저 정렬을 해주고, 이진 탐색을 통하여 찾고자 하는 값의

인덱스 번호를 출력해 줬다. 병합 정렬은 아래의 링크에서 확인할 수 있다.

병합 정렬(C언어)

 

※ 이진 탐색 코드

// ( 탐색할 배열, 찾을 값, 처음 인덱스, 마지막 인덱스)
int binary_search(int a[], int value, int m, int n) {
	if (m <= n) {
		int mid = (m + n) / 2;
		// 값을 찾은 경우 인덱스 번호 반환
		if (a[mid] == value) return mid;
		// 값이 mid 인덱스 위치의 값보다 큰 경우
		else if (a[mid] < value) return binary_search(a, value, mid + 1, n);
		// 값이 mid 인덱스 위치의 값보다 작은 경우
		else return binary_search(a, value, m, mid - 1);
	}
}

 

※ 병합 정렬 + 이진 탐색 코드

#include<stdio.h>

int sorted[8];

void merge(int a[], int m, int mid, int n) { 
	int i = m;
	int j = mid + 1;
	int k = m;

	while (i <= mid && j <= n) {
		if (a[i] < a[j]) {
			sorted[k] = a[i];
			i++;
		}
		else {
			sorted[k] = a[j];
			j++;
		}
		k++;
	}
	if (i > mid) {
		for (int t = j; t <= n; t++) {
			sorted[k] = a[t];
			k++;
		}
	}
	else {
		for (int t = i; t <= mid; t++) {
			sorted[k] = a[t];
			k++;
		}
	}
	for (int t = m; t <= n; t++) { 
		a[t] = sorted[t];
	}
}

void merge_sort(int a[], int m, int n) {
	if (m < n) {
		int mid = (m + n) / 2; 
		merge_sort(a, m, mid);
		merge_sort(a, mid + 1, n);
		merge(a, m, mid, n);
	}
	return;
}

int binary_search(int a[], int value, int m, int n) { // ( 탐색할 배열, 찾을 값, 처음 인덱스, 마지막 인덱스)
	if (m <= n) {
		int mid = (m + n) / 2;
		// 값을 찾은 경우 인덱스 번호 반환
		if (a[mid] == value) return mid;
		// 값이 mid 인덱스 위치의 값보다 큰 경우
		else if (a[mid] < value) return binary_search(a, value, mid + 1, n);
		// 값이 mid 인덱스 위치의 값보다 작은 경우
		else return binary_search(a, value, m, mid - 1);
	}
}

int main() {
	int arr[8] = { 8, 2, 5, 1, 3, 7, 4, 6 };
	merge_sort(arr, 0, 8 - 1); 
	for (int i = 0; i < 8; i++) {
		printf("%d ", arr[i]);
	}
	printf("\n%d", binary_search(arr, 3, 0, 8 - 1));
	return 0;
}